Supongamos que tenemos un modelo de programación lineal que resuelve:

Normalmente encontramos este tipo de modelos para resolver problemas de regresión u optimización continua. Al ser continuos, estos modelos no pueden resolverse de una forma en la que podamos considerarlos para fines de clasificación y que nos permitan crear, por ejemplo, una matriz de confusión para comparar su rendimiento con clases de datos reales. Para ello necesitamos considerar su solución desde un punto de vista de valores discretos.

Así, si queremos clasificar los puntos de un plano como pertenecientes a una clase o , podemos plantear el problema como uno en el que buscamos una línea recta que divida el plano y lo separe en dos regiones, donde cada una corresponde a una categoría de datos «bien definida».

Supongamos que tenemos el conjunto de datos:

Queremos hallar y , como:

Obsérvese que lo que hemos empezado a plantear como «bien definido» nos lleva implícitamente a considerar esa naturaleza discreta ya mencionada y que manifestamos en nuestra restricción con la condición ««. Esta es una forma simplificada de una máquina de vectores de soporte (SVM) lineal y rígida, y puede resolverse como un problema de programación lineal.

A fin de ilustrar mejor la idea, consideremos la representación de nuestro conjunto de datos en un espacio donde es representada por color (nuestra variable objetivo) y en un plano 2D (nuestro conjunto de observaciones, que en machine learning consideramos y usamos como datos de entrenamiento). El índice en las etiquetas de los ejes indica la columna de .

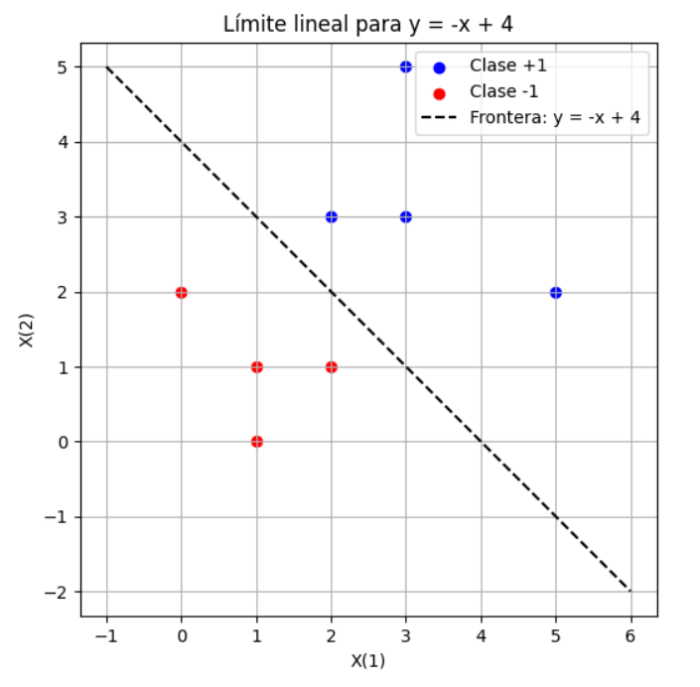
Idealmente, podríamos trazar una línea que nos permitiera separar las regiones en las que se ubican los datos de , por ejemplo :

Lo que nos sugiere que el problema tiene una solución y es posible separar ambos conjuntos de datos. Sin embargo, cuando usamos la programación lineal para separarlos con:

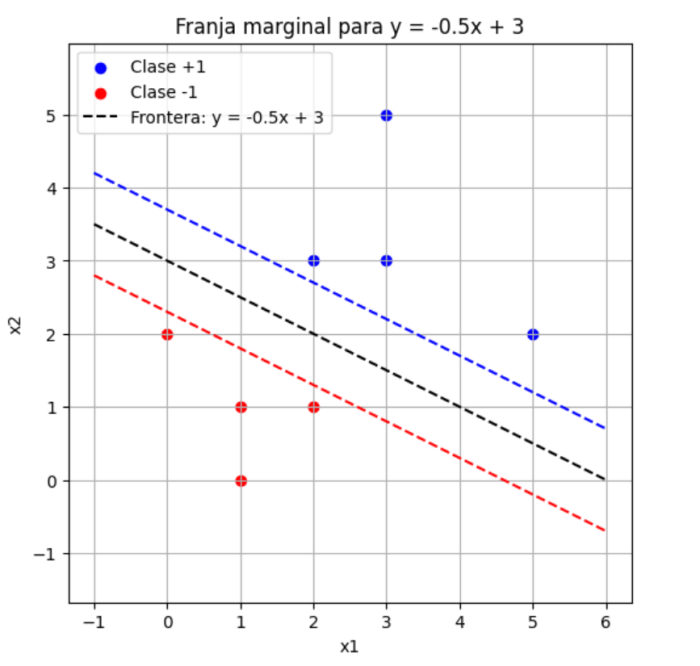
Lo que se demanda no es meramente una separación sino una determinada (mínima distancia) por cada punto del híper plano (recordemos que estamos trabajando al final con cantidades discretas y tres dimensiones) de manera que la desigualdad se satisfaga. No es suficiente decir «que el ‘punto’ está del lado correcto»; deben estar separados por una franja marginal unitaria.

Por cada punto de la clase , se requiere:

y por cada punto de la clase :

Esto genera la franja marginal entre y en la que ningún punto puede estar adentro. Ahora bien, para nuestro particular caso, veremos que tenemos un par de puntos muy cercanos a esta franja unitaria.

Para hacer frente a esta restricción, reformulamos nuestro modelo con variables de holgura, lo que permite puntos dentro del margen o incluso mal clasificados, a cambio de minimizar los errores totales.

Y así, agregamos la variable para permitir que puedan estar dentro de la franga marginal, o inclusive ser erróneamente clasificados.

donde:

Así, si tenemos datos, el problema tiene variables.

Aunque el modelo «duro» (nuestra primera versión) falló con el margen, al resolver el modelo de holgura, veremos que podemos encontrar una solución factible sin errores reales. Esto sugiere que existe un límite válido, pero el anterior era demasiado estricto al exigir un margen exacto.

Así entonces, el margen lineal es:

Un Jupyter notebook exponiendo esto (en inglés) más la implementación en Python junto con el uso de los solucionadores y optimizadores de modelos de programación lineal, está disponible en el hiperenlace al inicio de este párrafo.